二叉树

Posted on | In |
Words count in article: 1.6k | Reading time ≈ 7
二叉树、二叉树四种遍历、二叉搜索树、平衡二叉搜索树、红黑树

二叉树

  1. 二叉树的每个元素都恰好有两颗子树（可以是一颗或者为空）
  2. 二叉树中每个元素的子树是有顺序的，二叉树可以为空
  3. 二叉树有n个元素，有n-1条边
  4. 二叉树的高度是h，则至少有h个元素，至多有2^h-1个数据，此时称为满二叉树
  5. 从二叉树中删除编号为2^h-i个元素，称为完全二叉树
  6. 完全二叉树的重要特性：1）i=1，根；2）2i>n，该元素无左子树；3）2i+1>n，该元素无右子树
  7. 根节点和任一节点之间有唯一路径
  8. 根节点到任一节点的路径长度是该节点的深度，根节点深度永远是0
  9. 节点至最深节点的路径长度是该节点的高度
  10. 根节点的高度就是整棵树的高度

二叉树有四种遍历方法：

中序遍历是我们通常的书写形式，

前序遍历

1
2
3
4
5
6
7
8
9
10
template <class T>
void preOrder(binaryTreeNode<T> *t)
{
	if(t!=NULL)
	{
		visit(t);
		preOrder(t->leftChild);
		preOrder(t->rightOrder);
	}
}

中序遍历

1
2
3
4
5
6
7
8
9
10
template <class T>
void inOrder(binaryTreeNode<T> *t)
{
	if(t!=NULL)
	{
		preOrder(t->leftChild);
		visit(t);
		preOrder(t->rightOrder);
	}
}

后序遍历

1
2
3
4
5
6
7
8
9
10
template <class T>
void postOrder(binaryTreeNode<T> *t)
{
	if(t!=NULL)
	{
		preOrder(t->leftChild);
		preOrder(t->rightOrder);
		visit(t);
	}
}

层次遍历

在同一层中从左到右访问树的元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template <class T>
void levelOrder(binaryTreeNode<T> *t)
{
	arrayQueue<binaryTreeNode<T>*> q;
	while(t!=NULL)
	{
		visit(t);

		if(t->leftChild!=NULL)
		q.push(t->leftChild);
		if(t->rightChild!=NULL)
		q.push(t->rightChild);

		try{t=q.front();}
		catch(queueEmpty) {return;}
		q.pop();
	}
}

visit函数

1
2
3
4
5
template <class T>
void visit(binaryTreeNode<T> *x)
{
	cout<<x->element<<' ';
}

二叉搜索树BST

  1. 根节点>左节点 && 根节点<右节点
  2. 二叉树搜索树的中序遍历可以实现排序 ->amazing!

可以运行的四种遍历方法、二叉搜索树、获取树的高度和二叉搜索树的最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
#include <iostream>
#include <vector>
#include <stdlib.h>
#include <algorithm>
using namespace std;

typedef struct node{
    int data;
    struct node* left;
    struct node* right;
} Node;

typedef struct {
    Node* root;
} Tree;

//先序遍历
void preOrder(Node* node)
{
    if(node!=NULL)
    {
        cout<<node->data<<endl;
        preOrder(node->left);
        preOrder(node->right);
    }
}
//中序遍历
void inOrder(Node* node)
{
    if(node!=NULL)
    {
        inOrder(node->left);
        cout<<node->data<<endl;
        inOrder(node->right);
    }

}
//后序遍历
void posOrder(Node* node)
{
    if(node!=NULL)
    {
        posOrder(node->left);
        posOrder(node->right);
        cout<<node->data<<endl;
    }
}

void insert(Tree* tree, int value)
{
    //创建一个新的节点
    Node* node=new Node;
    node->data=value;
    node->left=NULL;
    node->right=NULL;

    if(tree->root==NULL)
        tree->root=node;
    else
    {
        Node* temp=tree->root;
        while(temp!=NULL)
        {
            if(value<temp->data)
            {
                if(temp->left==NULL){
                    temp->left=node;
                    return;
                }
                else
                {
                    temp=temp->left;
                }
            } else{
                if(value>temp->data)
                {
                    if(temp->right==NULL)
                    {
                        temp->right=node;
                        return;
                    }
                    else
                        temp=temp->right;
                }
            }
        }
    }
}

//获取二叉树的高度
int get_height(Node* node)
{
    if(node==NULL)
        return 0;

    else
    {
        int left_height=get_height(node->left);
        int right_height=get_height(node->right);
        return max(left_height,right_height)+1;
    }
}

//寻找二叉搜索树的最大值，二叉树左边的最大值和右边的最大值之间的最大值
int get_maximum(Node* node)
{
    if(node==NULL)
        return -1;

    int m1=get_maximum(node->left);
    int m2=get_maximum(node->right);
    int m=max(m1,m2);
    return max(m,node->data);
}

int main()
{
    vector<int> num{6,3,8,2,5,1,7};
    int len=num.size();
    Tree tree;
    tree.root=NULL;

    for(int i=0; i<len; ++i)
        insert(&tree,num[i]);

    //inOrder(tree.root);

    int height=get_height(tree.root);
    cout<<height<<endl;

    int maximum=get_maximum(tree.root);
    cout<<maximum<<endl;

    return 0;
}

平衡二叉搜索树

  1. 增加不同的平衡条件，二叉搜索树会表现出不同的效率
  2. 根节点的左子树的左子节点和右子树的右子节点为外侧，左子树的右子节点和右子树的左子节点为内侧
  3. 插入点位于外侧，可以采用单旋转操作；插入点位于内侧，可以采用双旋转操作

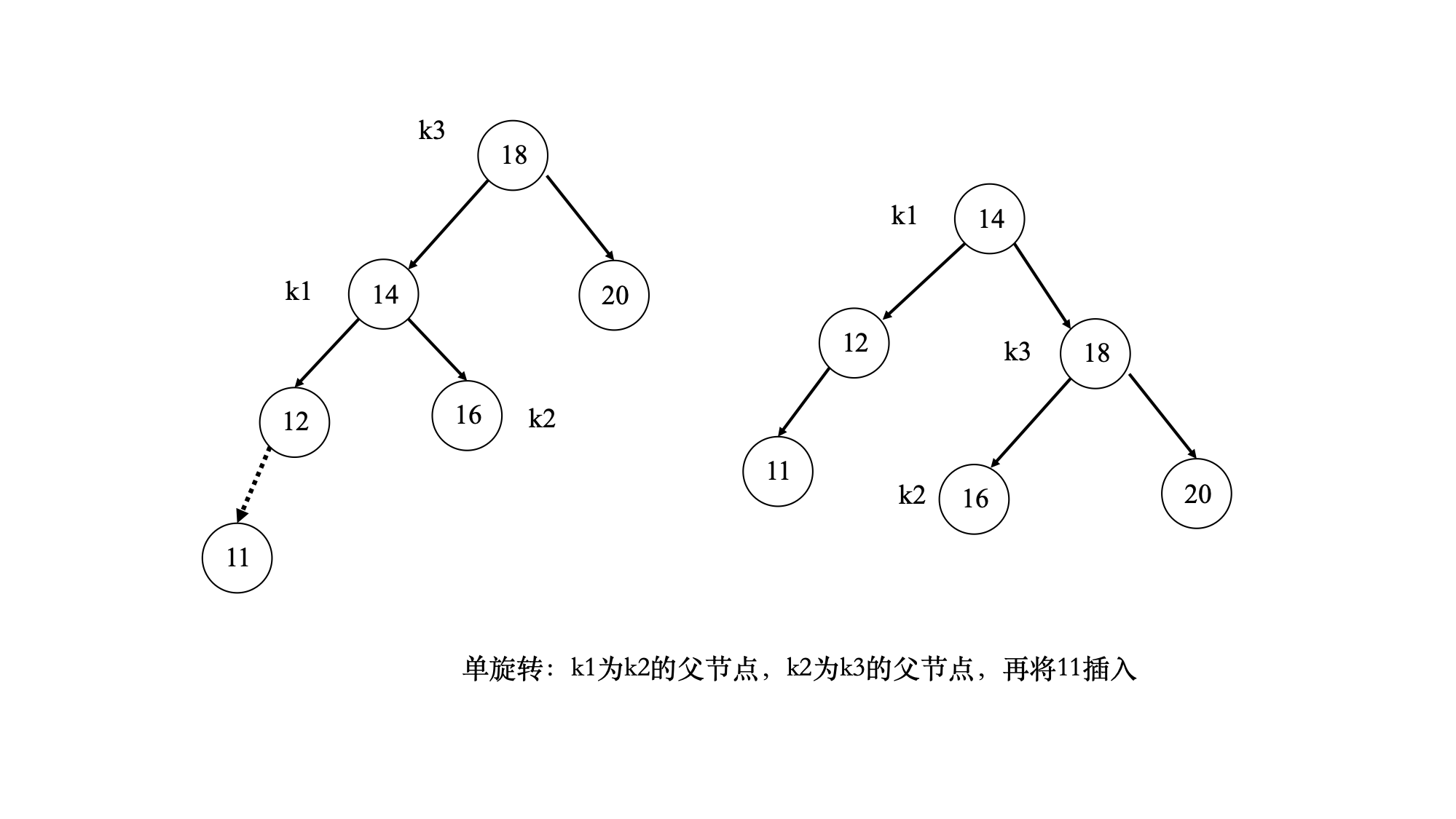
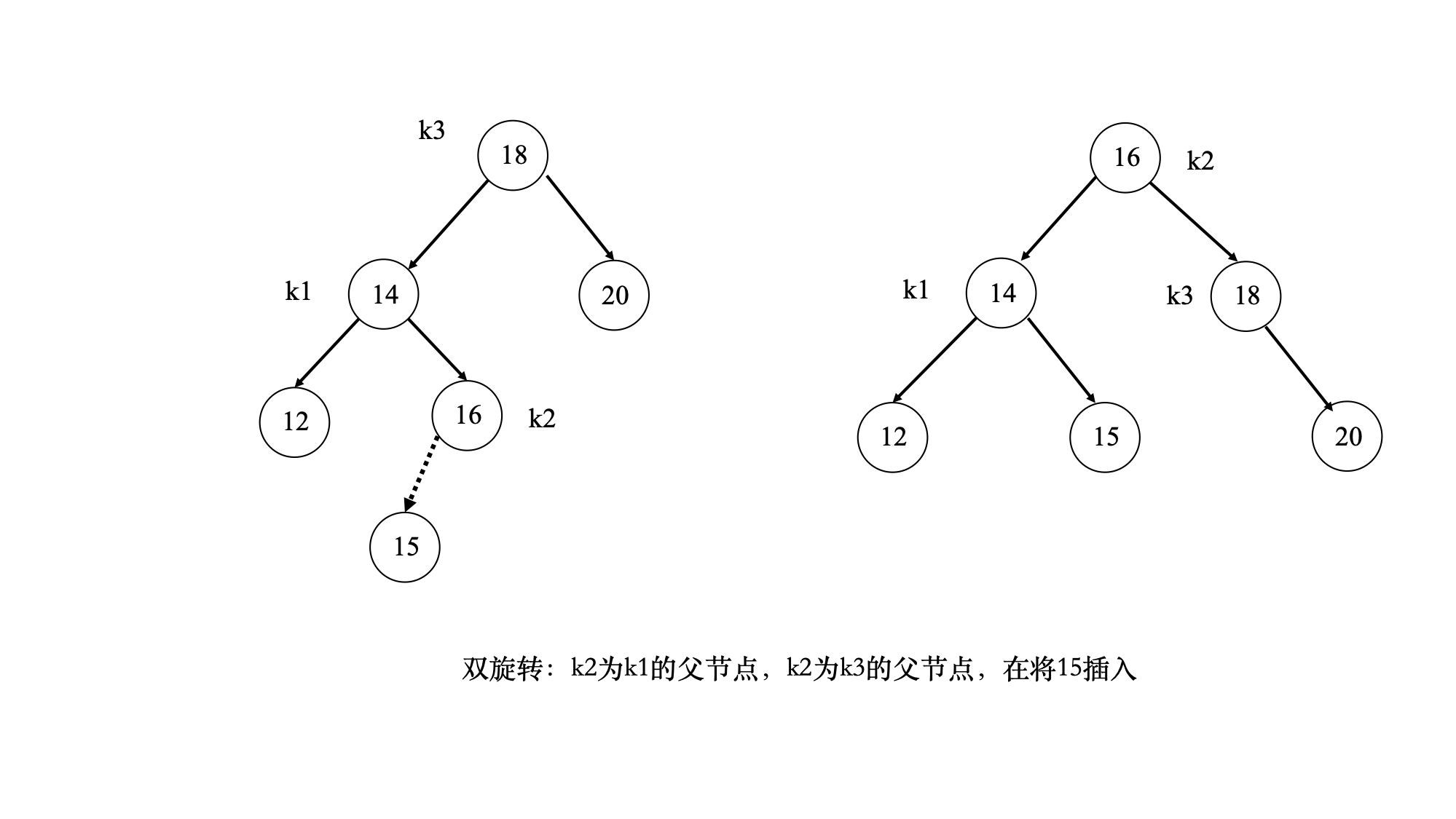
  4. AVL tree条件：任何节点的左右子树高度最多相差1，即保证对数深度保持平衡

RB-tree(红黑树)

  1. 红黑树的规则
  • 根节点是黑色的
  • 如果节点为红，则子节点必须为黑
  • 任一节点至树尾端的任何路径，所含的黑节点数必须相同
  • 新增节点必须为红，新增节点的父节点必须为黑，如果不能符合上述条件就必须调整颜色并旋转数型
  • 认为NULL节点为黑色
  1. 红黑树插入节点



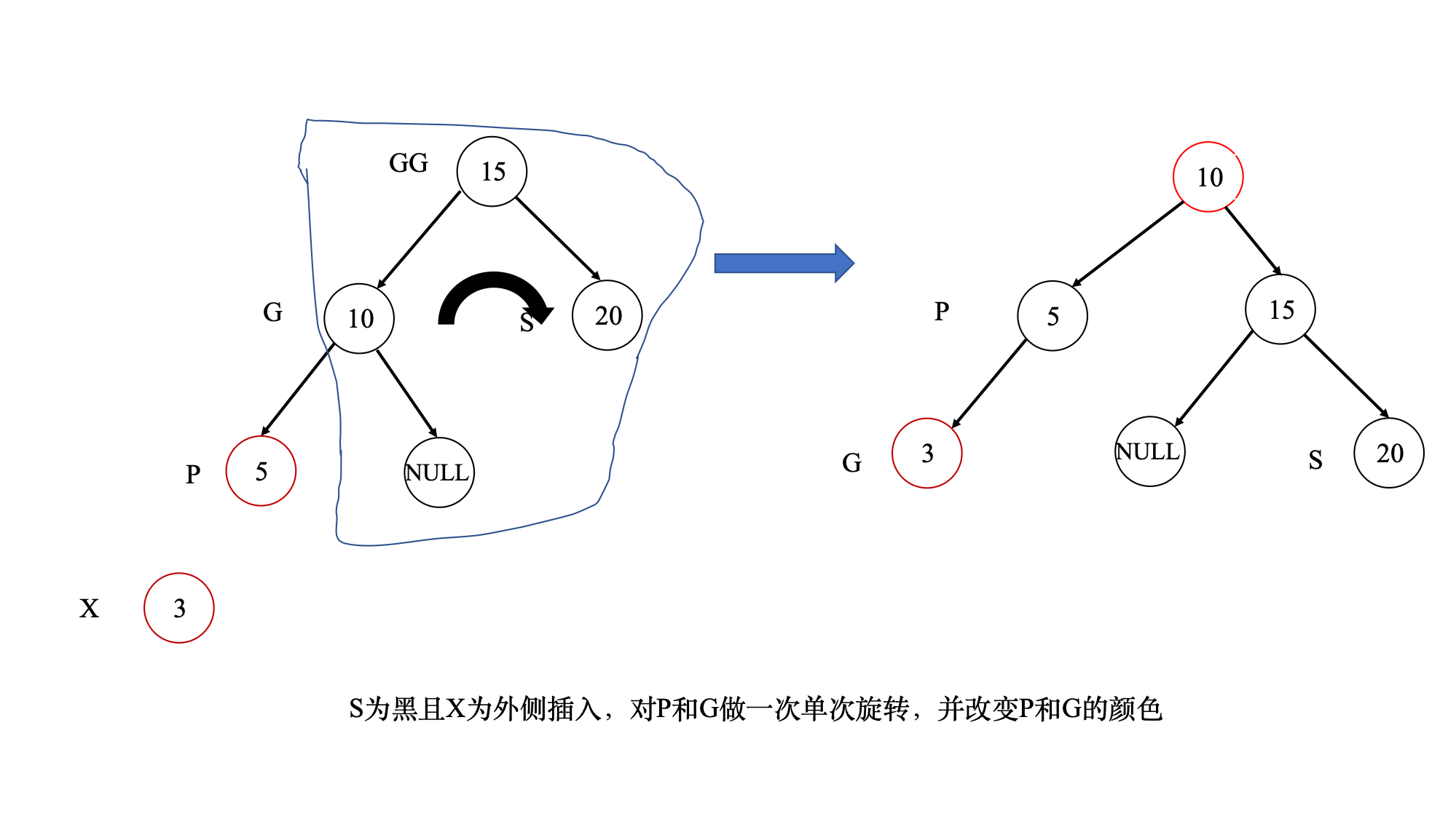
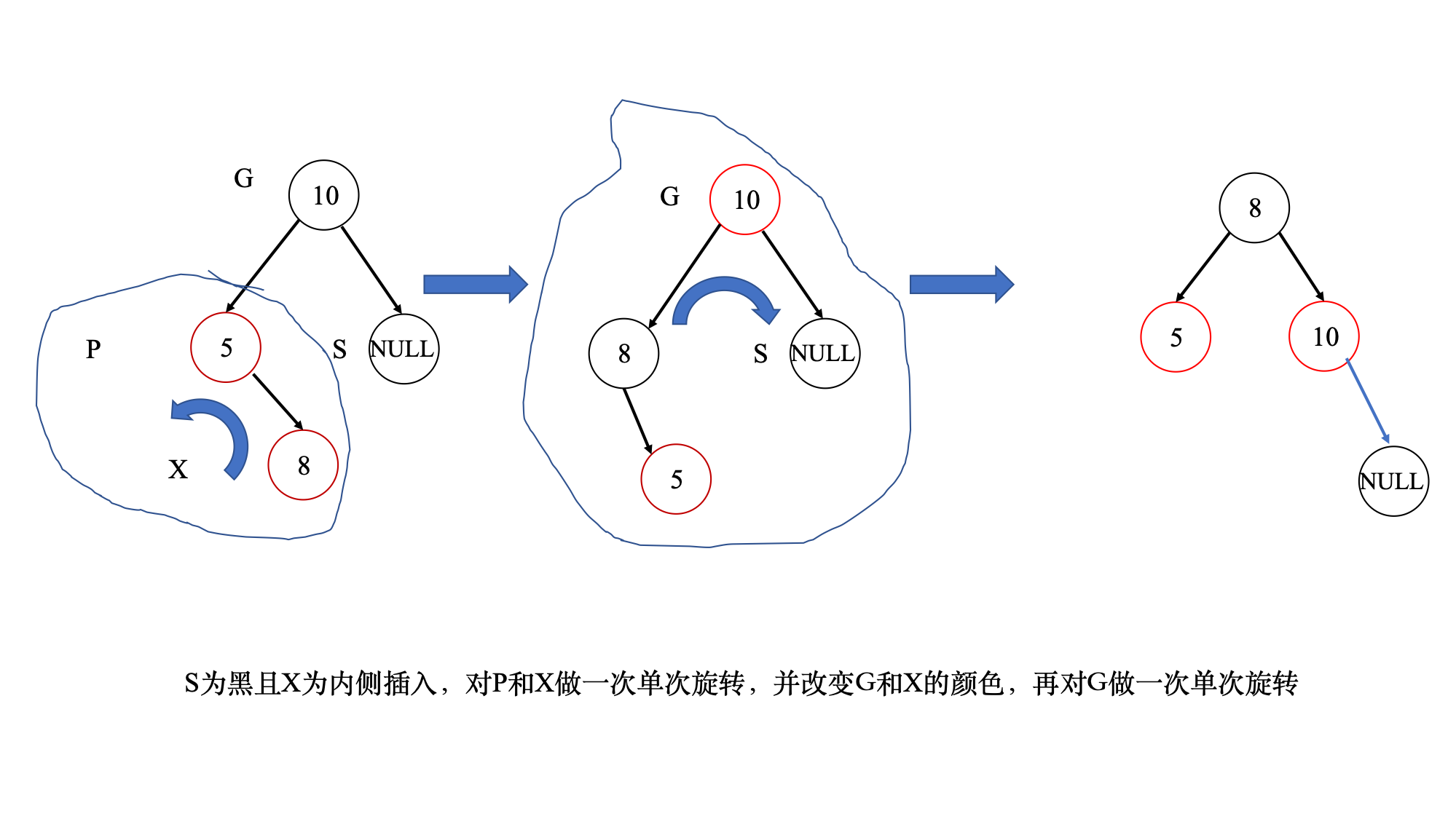
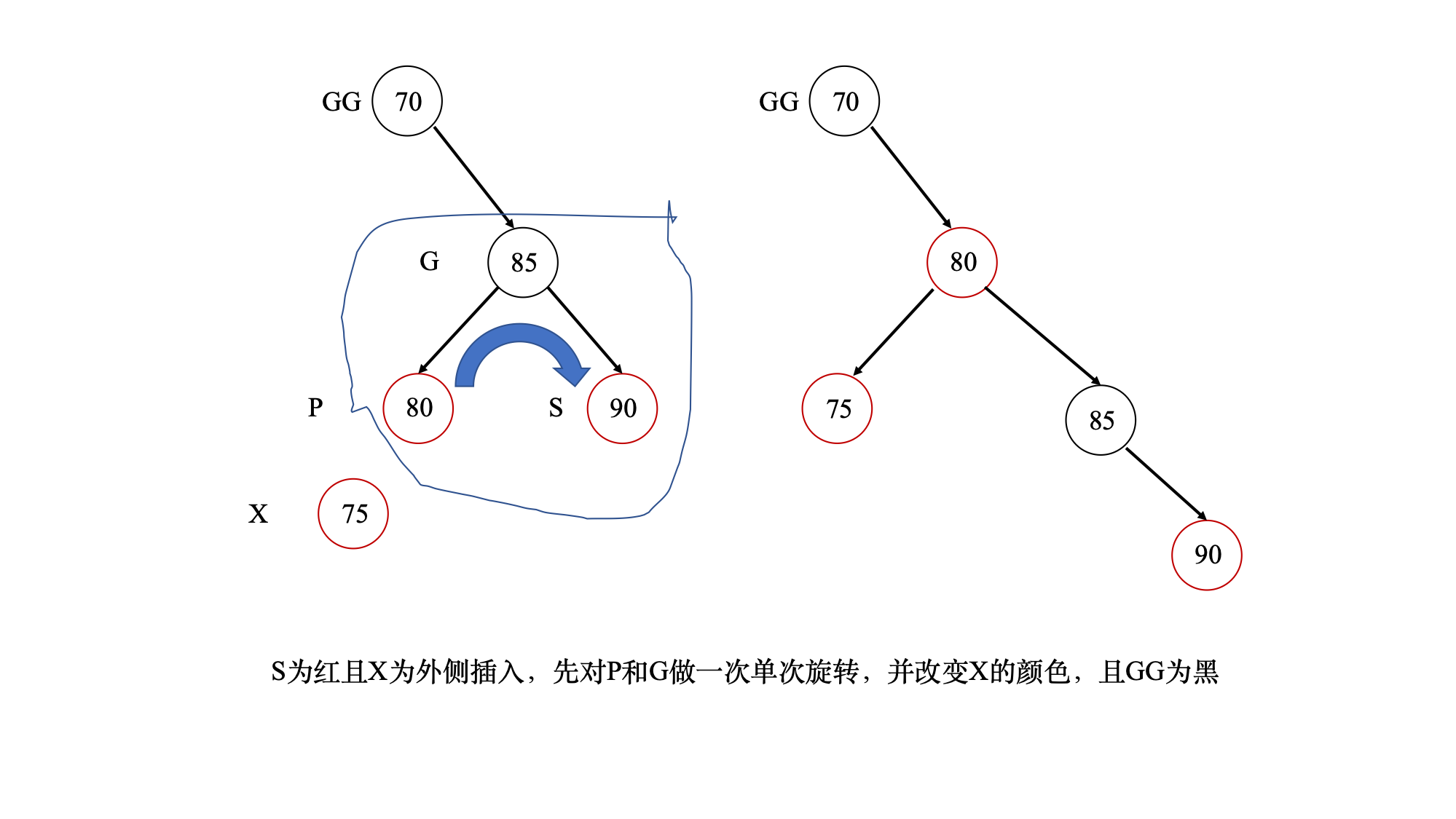
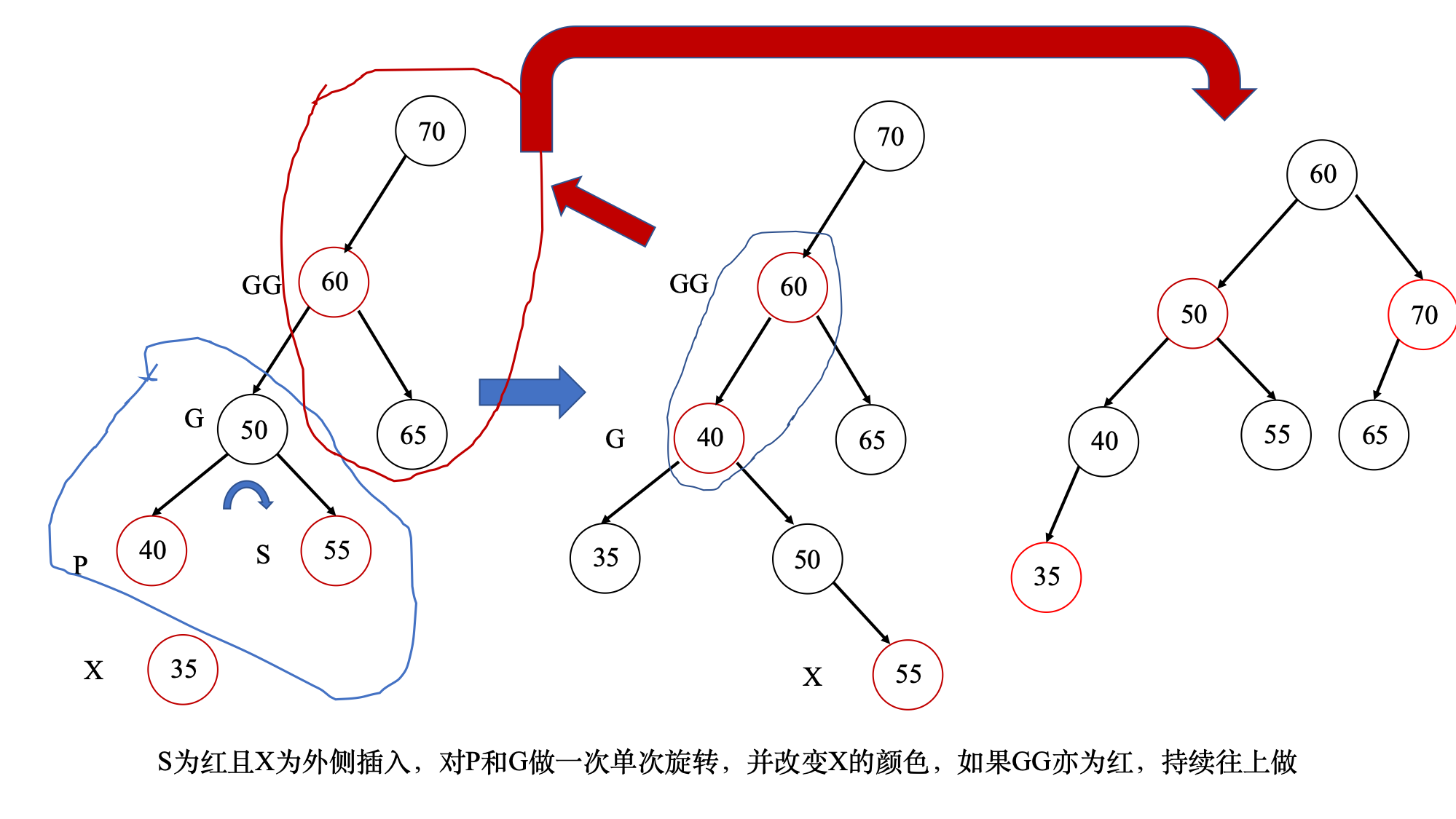
  2. 红黑树数据结构中有一个parent指针上溯到父节点
  3. 成员函数
  • get_node() 产生一个节点空间
  • put_node()
  • clone_node() 配置空间构造内容
  • destory_node() 析构内容释放内存
  • root() 根节点
  • minimum() 求取极小值
  • maximum() 求取极大值
  • begin() 红黑树最左边最小的节点
  • end() 红黑树的终点为header所指处
  • empty()
  • size()
  • max_size() return size_type(-1)
  • insert_unique() 将x插入到红黑树中，保持节点独一无二
  • insert_equal() 将x插入到红黑树中，允许节点重复
  • find() 寻找红黑树中键值为k的节点

  1. 红黑树的构造

    1
    2
    3
    4
    5
    6
    7
    8
    9
    rb_tree<int, int, identity<int>, less<int>> itree; //指定节点的键值、实值大小比较标准
    rb_tree(const Compare& comp=Compare()) : node_count(0), key_compare(comp) {init();}
    void init() {
    	header = get_node();	//产生一个节点空间，令header指向它
    	color(header) = __rb_tree_red; //令header为红色
    	root=0;
    	leftmost()=header;
    	rightmost()=header;
    }

  2. 真正执行插入操作的函数__insert(base_ptr x_. base_ptr y_, const Value& v); //x_是新值插入点，参数y_是插入点的父节点，参数v是新值

  3. 调整红黑树，将树的状态调整到符合红黑树的要求，重新令树形平衡，x是新增节点
    inline void __rb_tree_rebalance(__rb_tree_node_base* x, __rb_tree_node_base*& root)
  4. 左旋函数和右旋函数，新增节点必须是红节点，如果插入处的父节点也是红色，需要树形旋转
    inline void __rb_tree_rotate_left(__rb_tree_node_base* x, __rb_tree_node_base*& root);
    inline void __rb_tree_rotate_right(__rb_tree_node_base* x, __rb_tree_node_base*& root);
WhitneyLu wechat
Contact me by scanning my public WeChat QR code
0%